Lecture 0 - Overview of Reinforcement Learning in 30 Minutes

Overview of Reinforcement Learning in 30 Minutes

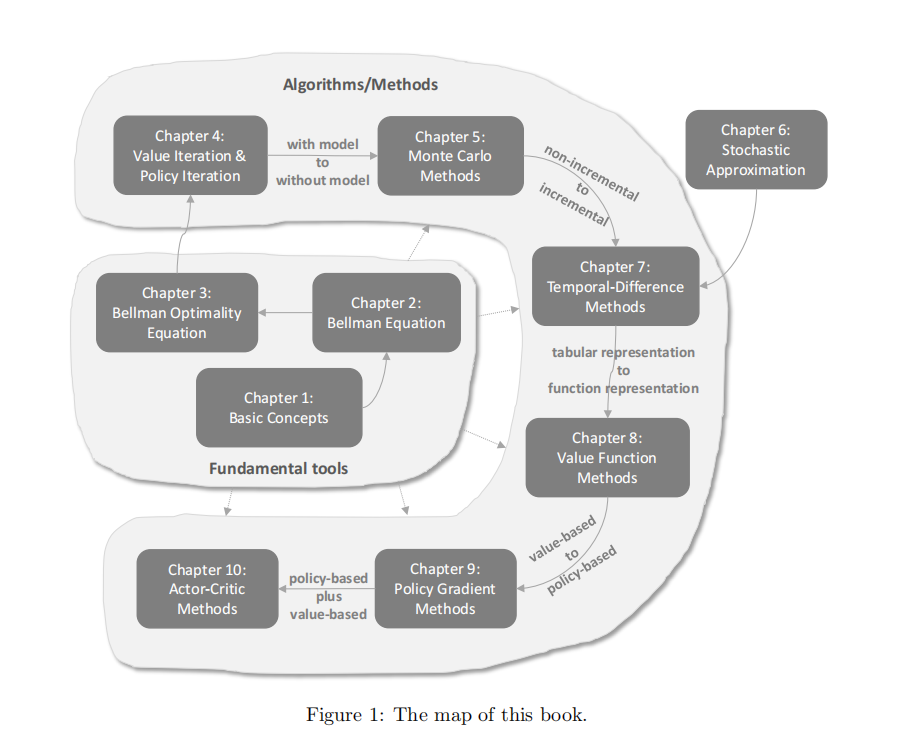
• Not just the map of this course, but also for RL fundations.
• Fundamental tools + Algorithms and methods.
• Importance of different parts.

1. Chapter 1: Basic Concepts
   • Concepts: state, action, reward, return, episode, policy,…
   • Grid-world examples
   • Markov decision process (MDP)
   • Fundamental concepts, widely used later
2. Chapter 2: Bellman Equations
   • One concept: state value

     $$\mathbb{v}_{\pi}(s) = \mathbb{E}[G_t | S_t = s]$$

   • One tool: Bellman equation

     $$\mathbb{v}_{\pi} = \mathbb{r}_{\pi} + \gamma P_{\pi} \mathbb{v}_{\pi}$$

   • Policy evaluation, widely used later
3. Chapter 3: Bellman Optimality Equations
   • A special Bellman equation
   • Two concepts: optimal policy $\pi^*$ and optimal state value $v^*(s)$
   • One tool: Bellman optimality equation

     $$\mathbb{v}^*(s) = \max_{\pi} (\mathbb{r}_{\pi} + \gamma P_{\pi} \mathbb{v}_{\pi}) = f(\mathbb{v})$$

     • Fixed-point theorem （不动点原理）
     • Fundamental problems
       • 最优策略、最优的 state value是否存在
       • 最优的 state value 是唯一的
       • 最优的策略可能是 deterministic，也可能是 stochastic
       • 一定存在确定性的最优策略
     • An algorithm solving the equation
   • Optimality, widely used later
4. Chapter 4: Value Iteration & Policy Iteration
   • First algorithms for optimal policies
   • Three algorithms:
     • Value iteration (VI) （值迭代）
     • Policy iteration (PI) （策略迭代）
     • Truncated policy iteration （截断策略迭代）
   • Policy update and value update, widely used later
   • Need the environment model
5. Chapter 5: Monte Carlo Learning
   • Gap: how to do model-free learning?
   • Mean estimation with sampling data

     $$E[X] \approx \overline{x} = \frac{1}{n} \sum_{i=1}^n X_i$$

   • First model-free RL algorithms
   • Algorithms:
     • MC Basic （基本的 MC 算法）
     • MC Exploring Starts （探索开始的 MC 算法）
     • MC $\epsilon$-greedy （基于 $\epsilon$-贪婪的 MC 算法）
6. Chapter 6: Stochastic Approximation
   • Gap: from non-incremental to incremental
   • Mean estimation
   • Algorithms:
     • Robbins-Monro (RM) algorithm （ Robbins-Monro 算法）
     • Stochastic gradient descent (SGD) （随机梯度下降算法）
     • SGD, BGD, MBGD
7. Chapter 7: Temporal-Difference Learning
   • Classic RL algorithms
   • Algorithms:
     • TD learning of state values （TD 学习状态值）
     • SARSA: TD learning of action values （TD 学习动作值）
     • Q-learning: TD learning of optimal action values （TD 学习最优动作值）
     • On-policy & off-policy （基于策略与非基于策略）
       • 强化学习中有两个策略：
         • behavior policy，用于生成经验数据
         • target policy，用于指导价值函数的更新
       • 如果 behavior policy 与 target policy 相同，即 $\pi = \mu$，则称为 on-policy learning（基于策略学习）
       • 如果 behavior policy 与 target policy 不同，即 $\pi \neq \mu$，则称为 off-policy learning（非基于策略学习）
     • Unified point of view
8. Chapter 8: Value Function Approximation
   • Gap: tabular representation to function representation
   • Algorithms:
     • State value estimation with value function approximation (VFA) （状态值估计与价值函数近似）:

       $$\min_{\pi} J(w) = \mathbb{E}[v_{\pi}(S) - \hat{v}(S,w)]$$

     • SARSA with VFA （Sarsa 算法与价值函数近似）
     • Q-learning with VFA （Q-learning 算法与价值函数近似）
     • Deep Q-learning
   • Neural networks come into RL
9. Chapter 9: Policy Gradient Methods
   • Gap: from value-based to policy-based
   • Contents:
     • Metrics to define optimal policies:

       $$J(\theta) = \overline{v}_{\pi}, \overline{r}_{\pi}$$

     • Policy gradient:

       $$\nabla J(\theta) = \mathbb{E}[\nabla_{\theta} \ln \pi(A | S) q_{\pi}(S, A)]$$

     • Gradient-ascent algorithm (REINFORCE):

       $$\theta_{t+1} = \theta_{t} + \alpha \nabla_{\theta} \ln \pi (a_t | s_t, \theta_t) q_t (s_t, a_t)$$

10. Chapter 10: Actor-Critic Methods
    • Gap: policy-based + value-based

      $$\theta_{t+1} = \theta_{t} + \alpha \nabla_{\theta} \ln \pi (a_t | s_t, \theta_t) q_t (s_t, a_t)$$

    • Algorithms:
      • The simplest actor-critic (QAC)
      • Advantage actor-critic (A2C)
        • 引入了一个 baseline $b(s_t)$，用于减少方差
      • Off-policy actor-critic
        • 使用 Importance sampling 的方法使得 QAC 由 on-policy 向 off-policy 转换
      • Deterministic actor-critic (DPG)